Помогите решить задачу по физике о вытекании воды из дырявых кастрюль
Задача
У меня есть две абсолютно одинаковые кастрюли с круглым донышком. В каждом донышке просверлено одинаковое число абсолютно одинаковых отверстий. Только в первой кастрюле все отверстия достаточно далеко отстоят друг от друга, а во второй, наоборот, образуют одну плотную группу.
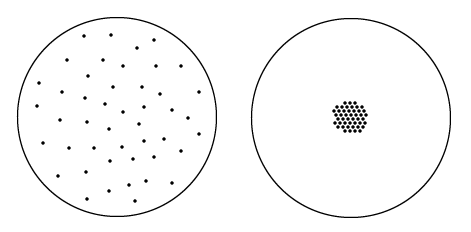
Плотная — значит, что расстояние между отверстиями меньше диаметра. Достаточно далеко, наоборот, значит, что расстояние между отверстиями в несколько раз больше их диаметра.
Теперь я наливаю в обе кастрюли одинаковый объем воды.
Вопросы:
- Эта вода вытечет из обеих кастрюль за одинаковое время или нет?
- Если время будет разным, значит на скорость вытекания воды влияет расположения отверстий. Тогда каким физическим законом описывается эта зависимость?
Я когда-то читал о том, что если группа отверстий расположена близко друг к другу, то их можно считать одним большим отверстием. Но не могу найти ни название, ни описание этого закона.
Закон Пуазейля
На форуме dxdy подсказали, что возможно здесь работает закон Пуазейля:
lel0lel: Если отверстия рядом, то суммарное вязкое трение будет меньше, так как соседние слои также находятся в движении. Относительно неподвижен только периметр всего семейства. А если отверстия далеко, то периметр каждого отверстия испытывает трение. В общем, чем-то напоминает формулу Пуазёйля.
Кроме того, посоветовали подумать над вопросом:
lel0lel: Вот ещё подумайте над таким вопросом: через какую систему будет проходить больший объём жидкости при условии, что перепад давления одинаков — через N параллельных труб радиуса r или одну трубу радиуса rN -½?
Закон Пуазейля формулируется следующим образом:
Объем Q жидкости, протекшей за секунду через поперечное сечение трубки, прямо пропорционален разности давлений r и r0 у входа в трубку и на выходе из нее и четвертой степени диаметра d трубки и обратно пропорционален длине l трубки и коэффициенту вязкости m жидкости:
Отсюда очевидный вывод: чем больше диаметр трубки и меньше ее длина, тем больше воды протечет через трубу.
Новые вопросы
После этого у меня возникли новые вопросы:
- Как найти критическое значение расстояния между отверстиями, такое, что если расстояния между отверстиями меньше данного критического, то мы их можем спокойно заменить на одно большое?
- Наоборот, как это критическое расстояние будет связано с диаметром отверстий?
- Что почитать по этому поводу — может статья какая-то хорошая есть?
lel0lel опять подсказал, что:
lel0lel: Это довольно сложный вопрос, который зависит от вязких свойств жидкости, а также от величины давления, то есть скорости вытекания отдельных струй, от диаметра самих отверстий. К тому же переход от состояния «как будто одно отверстие» к состоянию «много отдельных отверстий» будет достаточно плавным, то есть точной границы указать нельзя.
Если бы это было нужно для решения конкретной технической задачи (изготовление леек), то проще всего ответ получить экспериментально. Если же обязательно теоретическое решение, то без дифференциальных уравнений с граничными условиями не обойтись.
Отверстия микроскопического размера
Мои «кастрюли» крайне малы — диаметром меньше миллиметра с отверстиями порядка одного микрона. Отсюда возник следующий вопрос:
- Закон Пуазейля имеет какие-то ограничения по масштабу? Например, если отверстия имеют диаметр порядка нескольких сотен нанометров, то принципы Пуазейля будут для них все так же справедливы или здесь нужна уже какая-то другая гидродинамика?
И вот возможные объяснения:
sergey zhukov: Не знаю, если честно. По моему, все должно работать. Разве что вязкость жидкости на таких масштабах может оказаться несколько другой. Или же могут проявиться другие реологические свойства жидкости (отклонения от ньютоновой жидкости). Может, поверхностное натяжение как-то неожиданно проявится.
lel0lel: Конечно, свои ограничения формула имеет. Она получена для ламинарного течения, при условии, что длина трубы много больше участка, на котором создаётся параболический профиль скоростей.
Вообще, уже в этом смысле это не совсем наш случай, у нас длина отверстий маленькая. Поэтому формулу можно использовать только для первичного качественного анализа задачи.
На микро уровне будут играть роль и другие капиллярные эффекты. Можно сделать столь маленькие отверстия, что просачивание воды будет похоже на диффузию и ни о каком профиле скоростей говорить не придётся. Стало быть и формула будет непричём.
Наконец sergey zhukov подсказал:
sergey zhukov: Есть похожая задача — гидравлическое сопротивление перфорированных решеток. Здесь, правда, рассматривается довольно узкий диапазон расстояний между отверстиями, который вряд ли простирается до области, где отверстия перестают влиять друг на друга.
Формула Пуазейля хороша для расчета ламинарных потоков в трубах без учета сопротивления входа и выхода.
И посоветовал такую последовательность приближений
N параллельных труб площадью S каждая против одной трубы площадью NS.
N дроссельных шайб сечением S против одной дроссельной шайбы сечением NS. Расчет сопротивления дроссельной шайбы стандартный.
N дроссельных шайб сечением S против одной дроссельной шайбы с решетчатым отверстием общим сечением ячеек NS.
Решетка из N отверстий сечением S против дроссельной шайбы с решетчатым отверстием общим сечением ячеек NS.
Я тоже думаю, что во всех случаях во втором варианте сопротивление будет меньше.
Вывод
Таким образом предварительный вывод таков:
- Отверстия, расположенные близко друг к другу, будут пропускать воду быстрее.
- Однако, можно ли, и при каких условиях, заменить их на одно отверстия — мне пока не ясно.
Буду благодарен за любые объяснения.
