Это заметка-напоминалка о пхп-библиотеках, позволяющих найти сингулярное разложение матрицы (SVD — singular value decomposition).

Из Bellegarda (2005) Latent semantic mapping

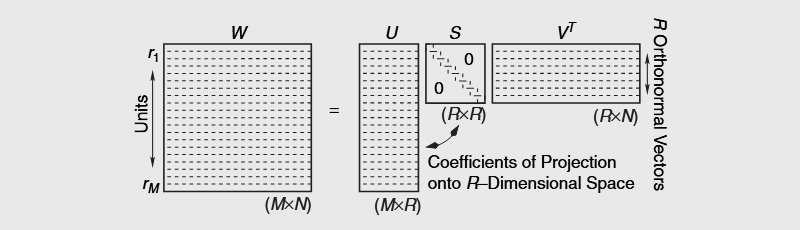
Наилучший вариант ↓

PHP — Singular value decomposition SVD Влада Колодки.
Без зависимостей. Один файл svd.php.

include "svd.php";

// Конструирую матрицу
$matrix = [['0.00', '0.00', '0.56', '0.56'. '0.00', '0.00', '1.00'], 
           ['0.49', '0.71', '0.00', '0.00'. '0.00', '0.71', '0.00'],
           ['0.49', '0.71', '0.00', '0.00'. '0.00', '0.71', '0.00'],
           ['0.72', '0.00', '0.00', '0.00'. '1.00', '0.00', '0.00'],
           ['0.00', '0.00', '0.83', '0.83'. '0.00', '0.00', '0.00']];

// Создаю класс для работы с матрицами
$matrixClass = new Matrix;

// Вычисляю SVD
$USV = $matrixClass->svd($matrix);

/*
 Получаю ассоциативный массив, в котором M = USV.
 ВНИМАНИЕ: матрица V уже транспонирована.

 $matrices['U'] = $U;
 $matrices['S'] = $S;
 $matrices['W'] = $W;
 $matrices['V'] = $this->matrixTranspose($V);
 $matrices['Rank'] = $rank;
 $matrices['K'] = $k;
*/

// Восстанавливаю исходную матрицу
$input = $matrixClass->matrixMultiplication($USV['U'] ,$matrixClass->matrixMultiplication($USV['S'], $USV['V']));
$input = $matrixClass->matrixRound($input);

Тяжеловесная библиотека ↓

MathPHP — Powerful modern math library for PHP
Огромное число разнообразных функций. Установка через композер.

Полный перечень функций для работы с матрицами.

use MathPHP\LinearAlgebra\Matrix;
use MathPHP\LinearAlgebra\MatrixFactory;

// Create an m × n matrix from an array of arrays
$matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
];
$A = MatrixFactory::create($matrix);

// Basic matrix data
$array = $A->getMatrix();  // Original array of arrays
$rows  = $A->getM();       // number of rows
$cols  = $A->getN();       // number of columns

// Matrix decompositions
// LU decomposition
$LU = $A->luDecomposition();
$L  = $LU->L;  // lower triangular matrix
$U  = $LU->U;  // upper triangular matrix
$P  = $LU-P;   // permutation matrix

// QR decomposition
$QR = $A->qrDecomposition();
$Q  = $QR->Q;  // orthogonal matrix
$R  = $QR->R;  // upper triangular matrix

// SVD (Singular Value Decomposition)
$SVD = $A->svd();
$U   = $A->U;  // m x m orthogonal matrix
$V   = $A->V;  // n x n orthogonal matrix
$S   = $A->S;  // m x n diagonal matrix of singular values
$D   = $A->D;  // Vector of diagonal elements from S

// Crout decomposition
$LU = $A->croutDecomposition();
$L  = $LU->L;  // lower triangular matrix
$U  = $LU->U;  // normalized upper triangular matrix

// Cholesky decomposition
$LLᵀ = $A->choleskyDecomposition();
$L   = $LLᵀ->L;   // lower triangular matrix
$LT  = $LLᵀ->LT;  // transpose of lower triangular matrix

// Eigenvalues and eigenvectors
$eigenvalues   = $A->eigenvalues();   // array of eigenvalues
$eigenvecetors = $A->eigenvectors();  // Matrix of eigenvectors

// Solve a linear system of equations: Ax = b
$b = new Vector(1, 2, 3);
$x = $A->solve($b);

Библиотека для машинного обучения ↓

PHP-ML — Machine learning library for PHP
Не по теме. Не понял, есть ли SVD.

Целоисчисленная матрица — это матрица, все элементы которой являются целыми числами.

Определитель целоисчисленной матрицы — тоже целое число. (Очевидно же.)

Используем класс целоисчисленных матриц, элементы которых могут принимать только значения из заданного множества целых чисел. (Такие матрицы называют богемными.)

Очевидно, что если множество возможных элементов матриц конечно, то и число возможных богемных матриц заданного размера тоже конечно.

Пусть мы ищем среди всех богемных матриц только те, определитель которых равен нулю. Ищем при помощи кода на Питоне. Определитель матрицы вычисляем так:

dt = np.linalg.det( a )

И вот тут возможна ошибка.

Если мы будем выбирать матрицы по условию dt==0, то получим неверный результат.

Using that test (dt==0) Python got the right number of [...] matrices when mdim=2 or mdim=3, but the test dt==0 failed a few times when mdim=4, and (after a long time computing) reported 15,015,617 singular matrices; the true number is 15,099,201. This is because np.linalg.det is computing the determinant from a numerical factoring (which introduces rational numbers and rounding error) and the roundoff error means that sometimes a zero determinant was not being reported as precisely zero.

Правильный результат получится если мы используем условие dt<0.5.

https://computational-discovery-on-jupyter.github.io/Computational-Discovery-on-Jupyter/Contents/bohemian-matrices.html#table-of-results