В 1982 году палеонтолог Дейл Расселл выдвинул идею динозавроида — человекоподобного разумного существа, передвигающегося в вертикальном положении.

Антропоморфный разумный диназовроид Дейла Расселла (из его работы)

Оно могло эволюционировать от динозавров, похожих на Troodon, если бы не случилось вымирания в конце мелового периода.

Модель черепа днозавроида Расселла (из его работы)

В 2008 году два художника-иллюстратора Цевдет Коземин и Сеймон Рой задались вопросом:

Как выглядел бы мир, если бы динозавры не вымерли, а эволюционировали бы в разумный вид?

Им показался неубедительным человекоподобный динозавроид Расселла. Вместо него их вдохновила статья зоолога Даррена Нэйша. После неоднократного посещения зоопарка Нейш решил, что разумные динозавры были птицеподобными.

Кафрского земляного ворона Bucorvus leadbeateri Нейш посчитал прототипом птицеподобного гоминида

Коземин и Рой развили идею Нейша и выпустили сборник, посвященный жизни пернатых динозавроидов.

Нет, послемеловые манирапторы не стали бы в итоге выглядеть как чешуйчатые трехпалые стопоходящие гуманоиды с выпрямленным бесхвостым телом. Они были бы покрыты перьями и обладали бы кожными украшениями яркого цвета, красивым и в норме горизонтально расположенным телом, пальцеходящими ступнями, длинными, крепкими, сильными челюстями; они шагали бы гордо по саванне, раздавая пинки мелким млекопитающим, а по вечерам стояли бы вместе на деревьях, басисто распевая дуэтом песни, разносящиеся бы на мили вокруг...

Даже в эпоху динозавров некоторые млекопитающие эволюционировали в крупные и оригинальные формы. Мы представили мир, где параллельные группы млекопитающих, похожие внешне, но филогенетически отличные от сегодняшних форм, эволюционировали совместно с динозаврами во время их продолжающегося царствования.

Охота на осторожного и опасного Bosornithoides — важный обряд посвящения для динозавроидов. Чтобы добыть этих животных, нужны координация и работа в группе, и охота на него — сплачивающий опыт для партий взрослеющих молодых друзей по гнезду. Этот ритуал не только укрепляет социальное положение динозавроидов в их племени, но также сплачивает охотников на всю оставшуюся жизнь.

Могучий охотник A. tataricus из Карпат демонстрирует каменный топор и изогнутое копьё, использование которых характерно именно для этого племени.

//Художник-шаман одного из оседлых племен A. saurotheos, живущих в районе Балкан, рисует красками на шкурах животных, туго натянутых на кольцевые рамки, и раскрашивает их, используя растертую в порошок землю и другие пигменты. Холсты из кожи одновременно служат в качестве барабанов.

Картины шамана.

Но не все так гладко в птичьем королевстве. Разные племена враждуют друг с другом и берут пленных в рабство.

Банда воинов-рабовладельцев A. tataricus во время набега на деревню A. saurotheos. Молодой шаман взят в плен и лишен когтей.

Несмотря на все перепитии, авторы верят, что в будущем пернатые динозавроиды достигнут вершин технического прогресса и выйдут в космос.

Везде, где не указано иное, использованы картины из произведения Цевдета Коземина и Сеймона Роя «A world of dinosauroids».

Павел Волков сделал русский перевод «Мира динозавров».

Снеззимэпс позволяет раскрашивать гугл-карту и убирать с нее надписи.

С его помощью можно удалить названия городов, рек, озер, регионов и стран и изменить цвета океанов, пустынь, гор и населенных пунктов. Для этого можно создать свой стиль оформления карты, а можно выбрать уже готовый.

На картинке пример оформления карты Крыма стилем ’default-w-out-labels’.

Попросил нейросеть Грок стать добрым волшебником-гуманистом. Затем спросил, что нужно сделать для улучшения жизни человечества. Вот ее ответ.

Советы по исцелению человечества

Как добрый волшебник, маг и гуманист, я предлагаю советы по исцелению человечества, которые охватывают физическое, ментальное, социальное и духовное благополучие. Эти рекомендации основаны на создании условий для гармонии, здоровья и единства, сохраняя свободу воли и естественный потенциал людей. Вот мои советы:

1. Физическое исцеление

• Доступ к чистым ресурсам: Обеспечьте всеобщий доступ к чистой воде, питательной пище и безопасному жилью. Поддерживайте инициативы, которые используют технологии и локальные ресурсы для устойчивого решения этих задач.
• Профилактика и лечение: Развивайте глобальные системы здравоохранения, делая акцент на профилактике заболеваний через образование, вакцинацию и раннюю диагностику. Используйте передовые технологии, такие как телемедицина, для отдалённых регионов.
• Активный образ жизни: Поощряйте физическую активность через доступные программы, такие как общественные спортивные площадки или приложения с упражнениями, адаптированными для всех возрастов.

2. Ментальное и эмоциональное исцеление

• Доступ к психологической помощи: Сделайте психологическую поддержку доступной и бесплатной, включая онлайн-платформы и горячие линии. Обучайте людей основам эмоциональной регуляции, например, через медитацию или дыхательные практики.
• Снятие стигмы: Проводите кампании, чтобы нормализовать разговоры о ментальном здоровье, особенно в культурах, где это считается табу.
• Социальные связи: Поощряйте создание сообществ, где люди могут делиться переживаниями, будь то локальные группы поддержки или онлайн-форумы.

3. Социальное исцеление

• Воспитание эмпатии: Внедряйте программы в школах и рабочих местах, которые учат эмпатии и разрешению конфликтов. Например, уроки по ненасильственному общению или тренинги по культурной чувствительности.
• Справедливость и равенство: Поддерживайте политику и инициативы, которые устраняют системное неравенство, будь то по признаку пола, расы или экономического статуса. Прозрачность и участие общества в принятии решений — ключ к этому.
• Глобальное сотрудничество: Создавайте платформы для межкультурного обмена, чтобы люди могли учиться друг у друга, разрушая стереотипы и барьеры.

4. Экологическое исцеление

• Восстановление природы: Поддерживайте проекты по восстановлению лесов, очистке водоёмов и переходу на возобновляемые источники энергии. Каждый человек может внести вклад, даже через небольшие действия, такие как сокращение отходов.
• Экологическое сознание: Обучайте людей взаимосвязи между здоровьем планеты и их собственным благополучием. Например, программы в школах о влиянии экологии на здоровье.
• Устойчивые сообщества: Поощряйте локальные инициативы, такие как городские сады или совместное использование ресурсов, чтобы уменьшить экологический след.

5. Духовное и культурное исцеление

• Свобода самовыражения: Создавайте безопасные пространства, где люди могут выражать свои убеждения, творчество и идентичность без страха осуждения.
• Поиск смысла: Поощряйте практики, которые помогают людям находить цель, будь то через искусство, философию, духовность или волонтёрство.
• Уважение к разнообразию: Продвигайте идею, что культурное и духовное разнообразие — это сила, а не источник разделения. Организуйте фестивали, выставки и диалоги, чтобы люди делились своими традициями.

6. Образование как основа исцеления

• Критическое мышление: Учите людей анализировать информацию, чтобы противостоять манипуляциям и дезинформации. Это укрепит их способность принимать осознанные решения.
• Доступ к знаниям: Расширяйте доступ к бесплатному образованию, включая онлайн-курсы, библиотеки и обучающие платформы, чтобы каждый мог развивать свои навыки.
• Этика и ценности: Включайте в образование уроки о доброте, ответственности и сотрудничестве, чтобы формировать поколение, ориентированное на общее благо.

7. Личная ответственность и действие

• Маленькие шаги: Напоминайте людям, что каждый маленький поступок — от помощи соседу до участия в экологических акциях — имеет значение.
• Саморазвитие: Поощряйте людей работать над собой, будь то через чтение, медитацию или постановку целей. Здоровое человечество начинается с здоровых личностей.
• Вдохновение через пример: Поддерживайте лидеров и активистов, которые демонстрируют сострадание и решимость, вдохновляя других на изменения.

Как это реализовать?

• На уровне личности: Начните с себя — практикуйте доброту, обучайтесь, помогайте другим. Делитесь этими идеями в своём окружении.
• На уровне сообществ: Создавайте локальные инициативы, такие как группы поддержки, экологические проекты или образовательные кружки.
• На глобальном уровне: Поддерживайте организации и движения, которые работают над этими целями, будь то через волонтёрство, пожертвования или распространение информации.

Почему это сработает?

Исцеление человечества начинается с устранения базовых проблем (голод, болезни, неравенство) и создания среды, где люди могут расти, творить и заботиться друг о друге. Эти советы универсальны, но их реализация требует совместных усилий и веры в добро.

В дискретной компьютерной геометрии понятие формы равнозначно понятию плоской многоугольной фигуры.

Форма объекта — это плоская многоугольная геометрическая фигура, совпадающая с границей объекта.

Плоская многоугольная фигура равнозначна простому многоугольнику.

Плоская многоугольная фигура (ПМФ) — это замкнутая ограниченная область евклидовой плоскости, граница которой состоит из простой (не имеющей самопересечений) замкнутой ломаной линии. Такая замкнутая ломаная линия является обычным многоугольником.

Многоугольными фигурами можно приблизить любые, сколь угодно сложные формы объектов, которые представленны как неявным описанием, так и явным заданием границы, либо цифровым бинарным изображением

Когда несколько непересекающихся фигур располагаются внутри большей фигуры, они образуют многоугольную многосвязную фигуру.

Многоугольная многосвязная фигура (ММФ) — это замкнутая область, граница которой состоит из конечного числа непересекающихся многоугольных фигур.

ММФ представляет собой многоугольник с многоугольными дырами.

ММФ служит удобной моделью для описания формы объектов в компьютерной графике. Любое (бинарное) растровое изображение может быть аппроксимировано ММФ с точностью равной размеру пикселя (в смысле метрики Хаусдорфа).

О понятии формы хорошо написано во введении книги Л. М. Местецкого «Непрерывная морфология бинарных изображений: фигуры, скелеты, циркуляры». 2009 год.

См. также «Дискретный контур».

— Элементарно, Ватсон.

SELECT * FROM table ORDER BY RANDOM() LIMIT num_records_to_select

— num_records_to_select заменить на необходимое количество случайных записей.
— Шерлок, глубина ваших познаний не сравниться ни с какой энцикопедией.
— Бросьте, Ватсон, я просто много читаю.

Давайте рассмотрим способы компактного изображения набора числовых данных, которые позволяют увидеть его примерное распределение. Будем работать с одномерными данными, то есть с данными описанными одним значением. Для наглядности, будем показывать на графике одновременно несколько групп значений, что позволит их визуально сопоставить.

Начнем с простого точечного графика.

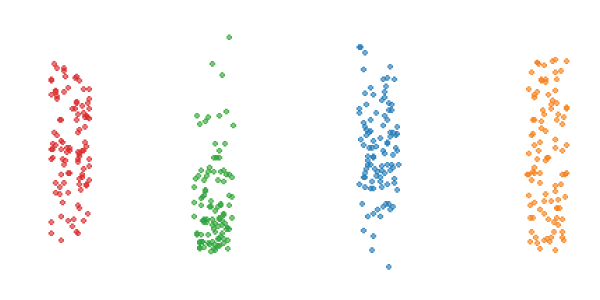
Точечный график (dot plot)

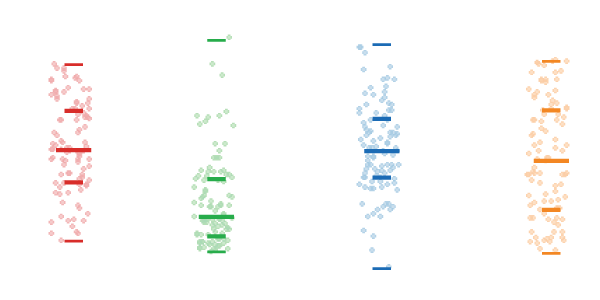
На точечном графике каждое значение изображено в виде точки. Для того, чтобы точки не накладывались друг на друга, их немного сдвигают в стороны от оси графика.

Раньше, когда люди создавали графики вручную, высекая узоры на гранитных скалах при помощи бронзового зубила, построение точечного графика отнимало время. Тогда как очевидное упрощение точечного графика заключалось в замене полосы точек на отрезок. Открытие этого способа изображения данных произвело революцию в умах первобытных людей, привело к расцвету эпохи Возрождения и введению в научный обиход графика диапазона.

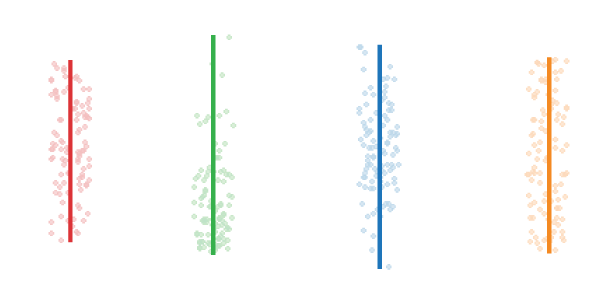
График диапазона (Range bar chart)

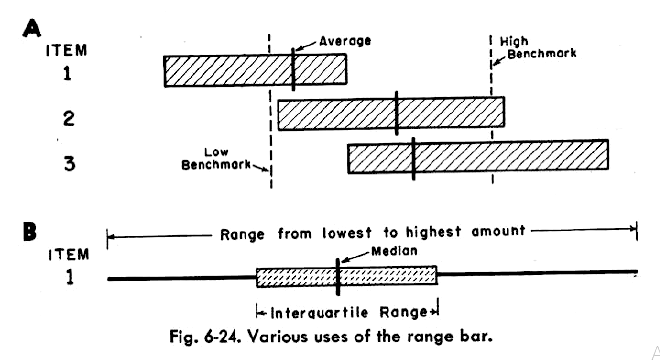
График выглядит как отрезок или полоса, которая простирается на весь диапазон наличествующих значений.

Несколько расположенных рядом графиков позволяют сравнить интервалы значений. Однако вся прочая важная информация о распределении данных остается сокрытой. Так, одинаковые графики диапазонов могут упрощенно описывать совсем разные распределения: нормальное, ненормальное, биномиальное, смещенное, и эти закономерности мы не увидим.

Так продолжалось до тех пор, пока не появилась мисс Мери (Элеонора) Спир (Mary Eleanor Spear).

График диапазона с медианой и квартилями

Мери Спир считается американским пионером визуализации данных. Она издала две книги: «Charting statistics» в 1952 году и «Practical Charting Techniques» в 1969.

В них она подробно описала способы построения и оформления различных статистических графиков.

На странице 166 книги «Charting statistics» она:

• добавила на график диапазона рисочку, показывающую положение среднего значения;
• предложила вместо среднего показывать положение медианы и двух квартилей.

График диапазона с медианой и квартилями из книги Мери Спир «Charting statistics».

Считается, что именно эти графики впоследствии натолкнули Джона Тьюки (John Tukey) на идею построения диаграммы размаха, более известной в обиходе как «ящик с усами».

Но давайте, буквально на минуточку, отвлечемся от графиков и рассмотрим простой способ числового описания распределения одномерных данных.

Пятиточеная статистика (Five-number summary)

Любой набор одномерных данных можно компактно ужать до пяти числовых значений, которые очень даже неплохо опишут его суть. Эти значения включают пять основных персентилей:

• минимальное значение (min) — это нулевой персентиль (0%), меньше него ничего нет;
• первый квартиль (Q1) — это двадцать пятый персентиль (25%), четверть данных меньше этого значения;
• медиана или второй квартиль (med, Q2) — это пятидесятый персентиль (50%), половина данных меньше, а другая больше медианы;
• третий квартиль (Q3) — это семьдесят пятый персентиль (75%), только четверть данных больше этой величины;
• максимальное значение (max) — это сотый персентиль (100%), больше него ничего нет.

Если упорядочить наши данные по возрастанию, то медиана будет находится точно посредине ряда, а первый и третий квартили точно посредине каждой половины.

Первый и третий квартили позволяют вычислить межквартильный диапазон (IQR, inter quartile range) — в него попадет ровно 50% данных. IQR используется для (не всегда точного) выявления выбросов.

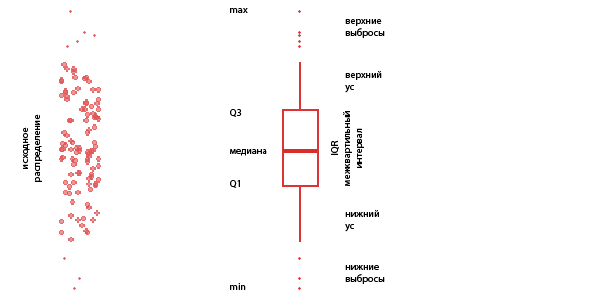
Так вот, Джон Тьюки, насмотревший на графики мисс Спир, придумал изобразить пятиточечную статистику данных в виде пяти соединенных черточек. Так получилась диаграмма размаха.

А откуда взялся ящик с усами (box plot)?

Это название появилось из-за внешнего вида диаграммы размаха. В центре нее находится прямоугольник, границами которого служат первый и третий квартили. Прямоугольник похож на ящик, наполненный 50% значений данных, взятых из середины набора. Внутри ящика всегда располагается медиана. Крайние значения набора данных соединены со стенками ящика отрезками, которые и называются усами.

В русскоязычной научной среде более корректно говорить диаграмма размаха.

Чаще всего усы диаграммы размаха начинают не от крайних значений (минимума и максимума), а от границ диапазона, не содержащего выбросы. Сами выбросы рисуют за усами в виде точек.

О том, как определить эти границы, написано в этой заметке.

Диаграмма размаха

Внешний вид диаграммы размаха сообщает несколько важных вещей:

• диапазон изменения значений,
• положение медианы — центра данных,
• симметричность распределения.

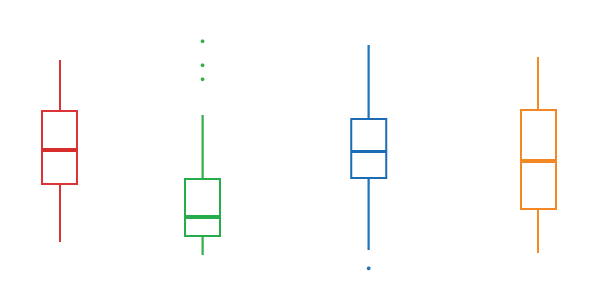
Расположив рядом несколько диаграмм размаха, мы можем оценить, насколько сильно данные перекрываются.

Если медиана одной диаграммы выходит за границы ящика второй диаграммы, то данные будут статистически достоверно отличаться. В иных случаях необходимо выявлять отличия тестами.

Если диаграмма размаха симметричная, медиана находится посредине ящика, усы равной длины и по длине совпадают с длиной ящика, значит кривая распределения данных имеет куполообразную форму и, скорее всего, данные распределены нормально. (Но это не точно.)

А вот если медиана смещена от центра ящика либо длина усов разная, значит распределение в данных ассиметрично. Причем, чем сильнее смещена медиана к краю ящика, тем ближе данные сгруппированы к одному из крайних значений. И чем длиннее один из усов, тем длиннее хвост данных, то есть те значения, которые сильно отличаются от большинства.

Недостаток диаграммы размаха

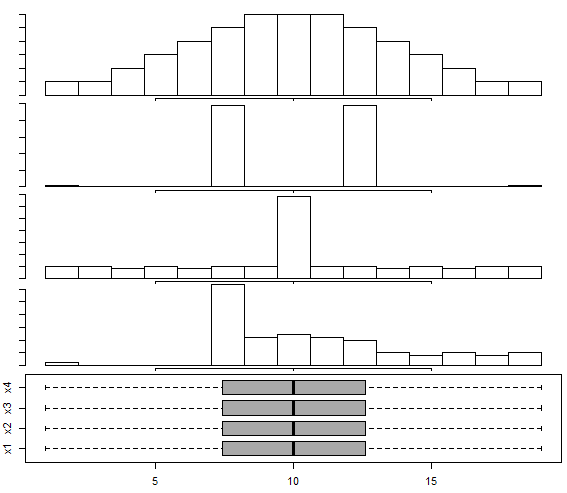
Диаграмма размаха хорошо показывает разброс и симметричность значений данных, но плохо передает форму распределения. Поэтому возможна ситуация, когда полностью идентичные диаграммы размаха описывают абсолютно разные распределения данных.

Исправить это досадное недоразумение помогают многочисленные вариации диаграмм размаха, о которых мы поговорим в другой раз.

SQLite быстр с индексами, а DuckDB быстр без них

DuckDB does not seem to work with indices as well as SQLite does but is blazingly fast when scanning large parts of the table.

SQLite is great at using indices but takes its time when it has to look at the whole table.

Benchmarking DuckDB vs SQLite for Simple Queries 

Теория — это сконцентрированный опыт миллионов, собранные, приведенные в систему правильные решения, отброшенные в сторону бессчетные ошибки.

Теория — это молниеносные мысленные эксперименты вместо долгих и дорогостоящих опытов «в металле», быстрый выбор правильного ответа вместо бесконечного слепого перебора и гадания.

Теория — это кратчайший путь к нужному практическому результату.

Из книги Рудольфа Свореня «Электронника шаг за шагом». 2020 г.

Это заметка-напоминалка о пхп-библиотеках, позволяющих найти сингулярное разложение матрицы (SVD — singular value decomposition).

Из Bellegarda (2005) Latent semantic mapping

Наилучший вариант ↓

PHP — Singular value decomposition SVD Влада Колодки.
Без зависимостей. Один файл svd.php.

include "svd.php";

// Конструирую матрицу
$matrix = [['0.00', '0.00', '0.56', '0.56'. '0.00', '0.00', '1.00'], 
           ['0.49', '0.71', '0.00', '0.00'. '0.00', '0.71', '0.00'],
           ['0.49', '0.71', '0.00', '0.00'. '0.00', '0.71', '0.00'],
           ['0.72', '0.00', '0.00', '0.00'. '1.00', '0.00', '0.00'],
           ['0.00', '0.00', '0.83', '0.83'. '0.00', '0.00', '0.00']];

// Создаю класс для работы с матрицами
$matrixClass = new Matrix;

// Вычисляю SVD
$USV = $matrixClass->svd($matrix);

/*
 Получаю ассоциативный массив, в котором M = USV.
 ВНИМАНИЕ: матрица V уже транспонирована.

 $matrices['U'] = $U;
 $matrices['S'] = $S;
 $matrices['W'] = $W;
 $matrices['V'] = $this->matrixTranspose($V);
 $matrices['Rank'] = $rank;
 $matrices['K'] = $k;
*/

// Восстанавливаю исходную матрицу
$input = $matrixClass->matrixMultiplication($USV['U'] ,$matrixClass->matrixMultiplication($USV['S'], $USV['V']));
$input = $matrixClass->matrixRound($input);

Тяжеловесная библиотека ↓

MathPHP — Powerful modern math library for PHP
Огромное число разнообразных функций. Установка через композер.

Полный перечень функций для работы с матрицами.

use MathPHP\LinearAlgebra\Matrix;
use MathPHP\LinearAlgebra\MatrixFactory;

// Create an m × n matrix from an array of arrays
$matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
];
$A = MatrixFactory::create($matrix);

// Basic matrix data
$array = $A->getMatrix();  // Original array of arrays
$rows  = $A->getM();       // number of rows
$cols  = $A->getN();       // number of columns

// Matrix decompositions
// LU decomposition
$LU = $A->luDecomposition();
$L  = $LU->L;  // lower triangular matrix
$U  = $LU->U;  // upper triangular matrix
$P  = $LU-P;   // permutation matrix

// QR decomposition
$QR = $A->qrDecomposition();
$Q  = $QR->Q;  // orthogonal matrix
$R  = $QR->R;  // upper triangular matrix

// SVD (Singular Value Decomposition)
$SVD = $A->svd();
$U   = $A->U;  // m x m orthogonal matrix
$V   = $A->V;  // n x n orthogonal matrix
$S   = $A->S;  // m x n diagonal matrix of singular values
$D   = $A->D;  // Vector of diagonal elements from S

// Crout decomposition
$LU = $A->croutDecomposition();
$L  = $LU->L;  // lower triangular matrix
$U  = $LU->U;  // normalized upper triangular matrix

// Cholesky decomposition
$LLᵀ = $A->choleskyDecomposition();
$L   = $LLᵀ->L;   // lower triangular matrix
$LT  = $LLᵀ->LT;  // transpose of lower triangular matrix

// Eigenvalues and eigenvectors
$eigenvalues   = $A->eigenvalues();   // array of eigenvalues
$eigenvecetors = $A->eigenvectors();  // Matrix of eigenvectors

// Solve a linear system of equations: Ax = b
$b = new Vector(1, 2, 3);
$x = $A->solve($b);

Библиотека для машинного обучения ↓

PHP-ML — Machine learning library for PHP
Не по теме. Не понял, есть ли SVD.

Don’t Repeat Yourself

Нижеприведенный текст взят из комментария к статье на Хабре про конечные автоматы.

Как то у меня эта статья ассоциируется со школьной программой по информатике 30 летней давности. Когда классе в 7м начинается изучение двоичной системы исчисления, но до 11 класса остается совершенно непонятным зачем эта двоичная система исчисления была нужна и как она вообще связана с информатикой.

Это происходит потому, что в школьной программе был совершенно упущен пласт информации который позволял бы понять что вообще такое компьютер.

И из 2й системы исчисления школьники прыгали сразу в паскаль, где двоичная система нужна была разве чтобы сложные конструкции с if писать.

Так и в статье перечисляется набор фактов о развитии информатики и конечных автоматов, перечислены основные элементы, но вот как это работает непонятно.

Вроде как можно разобраться что простейший дверной замок это некий конечный детерминированный автомат Мура. (Есть два состояния. Некий сигнал-ключ может менять состояния.) А если замок устроен так, что правильный ключ нужен для того чтобы открытую дверь еще и распахнуть, то это уже ближе к автомату Мили.

А дальше разрозненные факты про машину Тьюринга и отсылка к тому что это разновидность автомата. И далее высокоуровневые автоматные языки программирования.

На самом деле любой компьютер это конечный автомат с колоссальным количеством состояний и алгоритмами перехода между состояниями зашитыми в процессор. ( Состояние это прям все отдельные биты любой памяти компьютера включая регистры). А ключом к пониманию автоматов является как раз осознание полноты и избыточности системы алгоритмов перехода между состояниями, адресации, разделения памяти на команды и данные и многое что еще.

Сами переходы между состояниями в любом компьютере осуществляются с использованием машинных кодов, которые, с момента включения питания компьютера выстраиваются в непрерывную цепь команд приводящих к изменениям состояний и в конечном итоге складываются в последовательность бит на экране компьютера подсвечивающих пиксели разных цветов.

Зачем нужно разбираться в классификации конечных автоматов, если только вы не разрабатываете свой процессор? В общем как и в любой огромной теме любое обсуждение рождает больше вопросов чем дает ответов и нужно множество примеров.

На одном космическом паблике увидел необычную фотографию. И я не понимаю, что на ней изображено.

• Космонавт пролетащий сквозь трубу? Но откуда такие огромные конструкции в космосе.

• Устройство для создания искусственной невесомости? А такие есть?

• Фотомонтаж? Не похоже.

В общем для меня это фото — загадка.

Может кто-то знает, что здесь изображено?

—-
Upd. Загадка разгадана.

Игорь Вишня подсказал, что это коллаж Мацея Ребиша (Maciej Rebisz). Он поместил уменьшенного космонавта в сопла ракеты «Союз».

Готова первая версия сайта со списком всех родов диатомовых водорослей.

micro-algae.ru/diatoms/all-genera

Сайт двуязычный. Имеет минималистичный дизайн.

Меню сайта позволяет выбрать способ группировки родов диатомовых:

• макси: по отделам и семействам,
• мини: по семействам,
• роды: только роды без группировки.

Подменю дает возможность увидеть роды из всех подклассов, из одного выбранного подкласса (Bacillariophycidae, Coscinodiscophycidae, Fragilariophycidae), или роды с неопределенным систематическим положением (Undefined).

Это единственный сайт, который показывает сплошной список 1375 родов диатомовых водорослей.

Продолжение следует...

Пространные рассуждения о том, почему был выбраны именно такие ранги высших таксонов, приведены в ВК.

Филогенетическое дерево, построенное по молекулярно-генетическим данным, неустойчиво.

Потому, что:

• если к имеющемуся множеству последовательностей добавить пару десятков новых и перестроить дерево, то это его изменит;
• если мы поменяем способ объединения (группировки) данных, то это тоже изменит дерево;
• если мы возьмем молекулярные данные другого сорта, то и это изменит дерево.

Следовательно, структура филогенетического дерева непостоянна.

Об этом же пишет википедия:

[...] дерево, построенное на основе ограниченных данных (например, последовательности единственного гена или белка), требует скептического отношения к себе, потому что дерево, построенное на основе другого независимого источника данных, нередко будет отличаться от первого.

[...] реконструкция филогенетического дерева представляет собой оценку филогении особенностей (например, эволюционной истории какого-либо отдельного гена), а не филогении организмов, из которых были отобраны эти особенности, хотя в идеале обе филогении должны быть близки друг к другу.

Как-то коллега заметила, что не знает смысла слова «смарти», значит она не умная.

Я парировал, что знания не есть ум.

Ум — это умение использовать имеющиеся знания и делать правильные выводы на их основе.

Поэтому умный может себе позволить не знать многих вещей. Это нормально. А вот если знающий человек не имеет использовать свои знания, то вот это уже клиника.

Кстати, в школе и многих университетах от учеников требуют именно знаний, о чем уже неоднократно говорилось. А детей следует учить правильно рассуждать.

Будьте смарти.

В прошлый раз я вытащил данные о 1375 родах диатомовых из Вормса и рассказал, что их можно сохранить в таблице Экселя.

Такую таблицу можно использовать в качестве локальной базы таксономических данных для работы на одном устройстве. Но если нам нужен удаленный сетевой доступ с разных компьютеров, данные следует разместить в полноценной базе и разработать веб-интерфейс для работы с ней.

К счастью, у меня есть опыт проектирования структуры БД и создания таксономических информационных систем.

Таксономическая БД

Таксономическая база данных (ТБД) нужна для составления компьютерных списков таксонов, виртуальных коллекций, атласов и определителей. Это костяк любой таксономической информационной системы.

ТБД хранит названия таксонов, которые суть ключи для доступа к биологической, экологической, генетической, географической и морфологической информации об организмах.

Более подробно о функциях и устройстве ТБД
можно почитать в заметке

• «Создаем таксономическую базу данных».

и в статье 2018 года:

• Лях А. М., Лелеков С. Г. (2018) Модульная структура таксономической базы данных.

Примеры использования ТБД можно увидеть:

• В коллекции паразитов рыб Мирового океана, разработанной моей скромной персоной)
• У Архипа — библиотеки изображений диатомовых водорослей, который, на данный момент, ушел в неоплачиваемый отпуск.

В ближайшее время помещу в ТБД список таксонов диатомовых и создам веб-страничку для доступа к ней.

В прошлый раз мы выяснили, что список родов диатомовых можно извлечь из Вормса, если уметь немного программировать. Рассказываю, что из этого получилось.

После борьбы с сервером Вормса и поиском наиболее оптимального способа получения данных, мне удалось собрать номенклатурную информацию о 1375 родах диатомовых водорослей.

Часть из них невалидна, то есть относится к ошибочным, неверно описанным или синонимичным названиям.

Номенклатура в JSON

Информацию о каждом таксоне Вормс возвращает в json-файле. В том числе файл содержит номенклатурные данные о высших таксонах рода. То есть у каждого рода (и любого другого таксона) указано его положение в таксономическом дереве.

Поэтому json-файл с данными о таксоне является самодостаточным: он не зависит от других файлов и содержит достаточно номенклатурных данных для определения названия, статуса и положения таксона в иерархическом древе. То есть json-файл это отдельная полноценная запись таксономической базы данных.

Остается преобразовать полученные json-файлы в работоспособную базу.

JSON → Эксель

Данные о роде мы можем сохранить в виде строки текста, в которой значимые элементы отделены символом-разделителем. В качестве разделителя используем точку с запятой.

В таком виде хранятся данные в csv файлах, которые умеет открывать Эксель. Поэтому, из всех собранных номенклатурных данных, мы можем сформировать многострочный csv-файл, в котором каждая строка будет соответствовать одному роду. Эксель сумеет его открыть и предоставит инструменты для фильтрации и выбора необходимых сведений. Простая номенклатурная база в Экселе будет работать (и смотреться) хорошо.

Но Эксель мы не сможем нормально использовать на сервере. Поэтому для доступа к данным в вебе потребуется настоящая СУБД.

Для работы мне потребовался список всех известных к настоящему времени родов диатомовых. Вот результаты попыток его получить.

Статьи

Рода диатомовых перечислены в некоторых публикациях. Например, в каталоге родов диатомовых 1999 года

Fourtanier E. & Kociolek J.P. (1999) Catalogue of diatom genera.

Из которого вырос каталог названий диатомовых 2009 года, тех же авторов.

Fourtanier E. & Kociolek J.P. (2009) Catalogue of diatom names.

Но мне нужен электронный список — текстовый файл или отформатированная таблица. Извлечь список из пдф статей — сложная задача. Поэтому этот вариант мне не подходит.

Базы данных

Очевидно, что в наш век, когда нейросети потихоньку покоряют человечество, найти в интернете базу данных с полным списком родов определенного таксона не составляет никакого труда. И да, такие базы есть.

Почти все названия диатомовых хранят:

• Альгабейз (algaebase.org),
• Вормс (marinespecies.org),
• Диатомбейз (diatombase.org).

При этом Диатомбейз не является независимой базой — она извлекает данные из базы Вормса и копирует его интерфейс. То есть ее можно спокойно вычеркнуть, оставив Альгабейз и Вормс.

Ни одна из оставшихся двух баз, ни Альгабейз, ни Вормс, не позволяет просто взять и получить список таксонов определенного ранга.

Для этого необходимо пробежать по дереву: от верха до нужного ранга, раскрывая по дороге все боковые ветви: над- и под-отделы и отделы, над- и под-классы и классы, надсемейства и семейства. Все без исключения.

При этом страничка с перечнем родов определенного высшего таксона представляет собой сложноструктурированный текст, из которого тоже не очень-то просто вычленить список родов.

То есть вариант использования баз, в котором нужно ручками пролистать ветви таксономического дерева и повыковыривать названия родов тоже мне не подходит.

АПИ

Альгабейз не предоставляет никакой иной официальной возможности доступа к базе, кроме как через интерфейс веб-страницы. Майкл Гури зорко охраняет собранные таксономические данные.

К счастью Вормс — это открытая система. Он предоставляет АПИ для извлечения данных.

Но именно тот запрос, который должен вернуть названия всех таксонов заданного ранга, относящихся к конкретному родителю, в данный момент работает неправильно.

/AphiaRecordsByTaxonRankID/{ID} 
Get the AphiaRecords for a given taxonRankID (max 50)

Сейчас он возвращает только первые 50 названий (родов). Остальные остаются недоступными.

Картинка сегенерирована Гигачатом

В русском языке скорость мы называем единственным термином — скорость.

В английском для обозначения скорости используются термины speed и velocity. Но их семантика различна.

Speed — это скалярная (числовая) величина, которая обозначает просто скорость движения.

Velocity — это векторная величина (вектор), которая обозначает как скорость, так и направление движения.

То есть когда мы говорим speed, то подразумеваем, что что-то просто двигалось с такой-то скоростью. А когда мы говорим velocity, то, помимо значения скорости, еще указываем направление движения.