Коллега попросил помочь с выполнение дисперсионного анализа. Рассказываю, что получилось.

У нас есть три ряда длин раковин моллюсков, полученные в три разных года: 1981, 1998 и 2012. Мы хотим узнать, есть ли статистически достоверное различие между средними длинами в каждый период или нет? Расскажу, как это сделать.

Фрагмент исходных данных

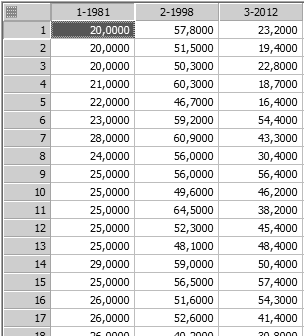
Сначала посмотрим на статистическое описание данных.

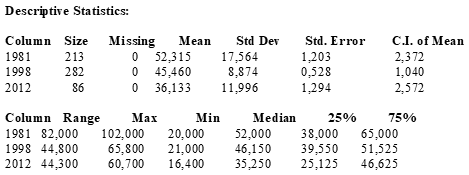
Средние и медианы неплохо отличаются, наверное различия все-таки есть.

Потом построим диаграммы размахов, в простонародье — ящики с усами.

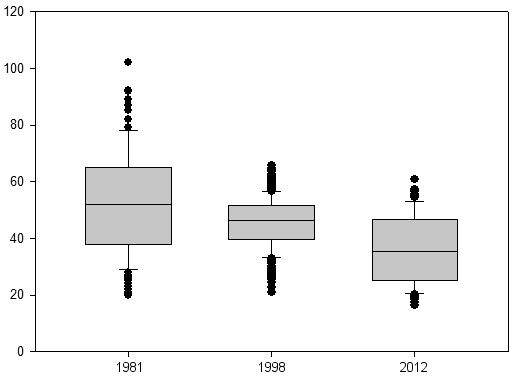
Второй и третий ящики практически полностью пересекаются с первым. Значит различия недостоверны?

Теперь попробуем попарно сравнить средние при помощи t-теста стьюдента: первое со вторым, второе с третьим и третье с первым. Наши данные независимы, потому что мы каждый раз измеряли разных моллюсков. Значит применим t-тест для независимых выборок. Но предварительно проверим данные на нормальность. Если выборки имеют нормальное распределение, используем t-тест. Если ненормальное, прочитаем Сергея Мастицкого (стр. 36):

Если значение распределены ненормально, применение параметрического t-теста будет часто приводить к искаженным результатам. В таких случаях следует воспользоваться непараметрическим аналогом теста стьюдента. Например можно использовать u-тест манна-уитни.

Вперед.

Попарные сравнения u-тестом манна-уитни

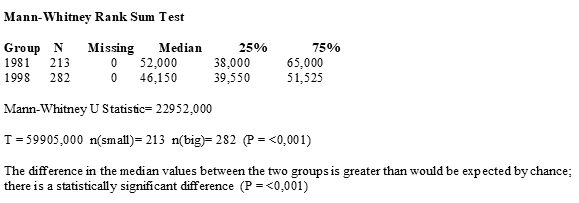
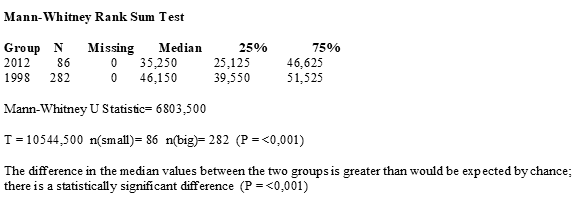
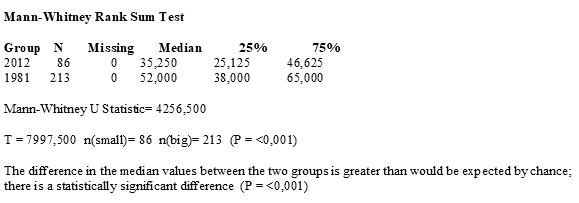
Попарные сравнения показали отличия средних.

А теперь читаем книгу Мастицкого уже на стр. 43:

Тесть стьюдента и его непараметрические аналоги предназначены для сравнения исключительно двух выборок. Очень часто исследователи допускают ошибку: используют t-тест для попарных сравнений более двух выборок.

Надо же, оказывается мы допустили частую ошибку статистических профанов. И как нам быть?

Для избежания данной ошибки необходимо использовать дисперсионный анализ.

Алилуя! Но теперь надо прочитать хорошие книги о дисперсионном анализе?

Нет, совсем не обязательно. Автоматизация статистических вычислений, в настоящее время, достигла таких высот, что вам всего лишь нужно нажать правильные кнопки. Все остальное сделает машина. Например так работает Сигмаплот. Он сам проверит данные на нормальность и выберет правильный тип дисперсионного анализа.

Наши данные оказались ненормальными, поэтому Сигмаплот предложил непараметрический дисперсионный анализ крускала-уолиса (H-тест) и объяснил полученные результаты.

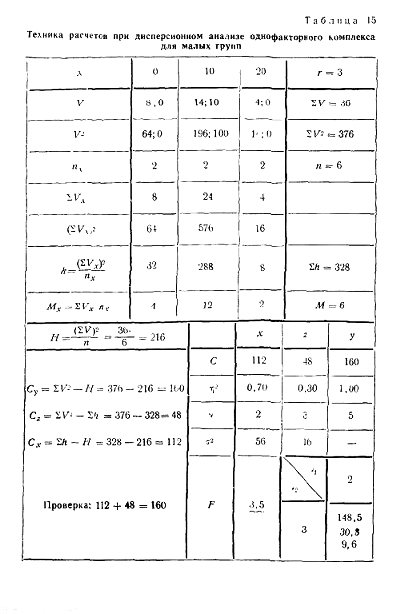
Если бы мы воспользовались Статистикой или Эр, нам пришлось бы интерпретировать полученные цифры. Для этого следует хорошо разобраться в дисперсионном анализе и сопутствующих методах. То есть пройти хороший курс биометрии.

Но тот-кто-знает, что «интерфейс — зло» и «потеть должна машина», тот выберет способ «нажал на кнопку и получил развернутый ответ». Мозги, в этом случае, пригодятся для интерпретации ответа.

Пирамида Лебедева

Выбирайте сами. И, да — это не реклама Сигмаплота. Просто мне понравилось, как он интерпретировал результат.

Книги, в любом случае, читать полезно.

М. попросила проверить, достоверно ли различие между длинами раковин моллюсков? Причем с помощью дисперсионного анализа. А я, как это бывает, позабыл как его выполнить. Чтобы вспомнить, принялся читать книги. И родился у меня рейтинг прочитанного.

Не мудрствуя лукаво, разделил книги на две категории: многоразовые — к которым буду обращаться и перечитывать, и одноразовые — пролистал и выбросил в корзину.

Многоразовые книги

Мастицкий С. Э. (2009) Методическое пособие по использовании программы Statistica при обработке данных биологических исследований. Минск: Ин-т рыбного хозяйства.

Прекрасное руководство для прикладных статистов.

Автор кратко описывает для каких рядов данных подходит тот или иной прием и рассказывает, как их выполнить в «Статистике». Книга полезна, даже если вы не используете «Статистику».

Любищев А. А. (1986) Дисперсионный анализ в биологии. М.: Изд-во Моск. ун-та.

О том как планировать эксперименты и интерпретировать результаты без помощи компьютера.

Книга написана в середине 20-го века. Написано легко, с разбором многочисленных примеров и методикой ручных вычислений. Буду не раз к ней возвращаться.

Плохинский Н. А. (1960) Дисперсионный анализ. Новосибирск: Изд-во СО АН СССР.

Дисперсионный анализ на бумаге.

Ясно и прекрасно.

Одноразовые книги

Аренс Х., Лёйтер Ю. (1985) Многомерный дисперсионный анализ / Пер. с немецкого. М.: Финансы и статистика.

Полезно, кратко, по делу.

Книга попала в одноразовые, потому что ее основная аудитория — программисты, которые собираются писать софт для стат. анализа с нуля.

Маркова Е. В., Денисов В. И., Полетаева И. А., Пономарев В. В. (1982) Дисперсионный анализ и синте планов на ЭВМ. М.: Наука.

За деревьями леса не видно.

Много деталей, но не всегда ясна суть. Ориентирована на программистов, на что и указывает название.

Шеффе Г. (1980) Дисперсионный анализ / Пер. с английского. Изд. второе. М.: Наука. Гл. ред. физ.-мат. лит-ры.

Сложно, для истинных математиков.

Книга переполнена формулами, определениями и доказательствами. Написана для математиков, которые хотят досконально во всем разобраться и, возможно, сделать лучше. Остальные не увидят здесь сути анализа.

Яковлев В., Яковлева О. (2015) Дисперсионный анализ в Excel. Lap Lambert Acad. Publ.

Хрень полная.

Не тратьте время — выбрасывайте в корзину, не читая.

Рейтинг отражает мое лично впечатление от указанных книг. Ваше мнение может быть другим.

Читайте книги.